Silhouette and Stereo Fusion
for 3D Object Modeling
Carlos Hernández Esteban and Francis Schmitt
Signal and Image Processing Department, CNRS UMR 5141
Ecole Nationale Supérieure des Télécommunications, France
|
Download: pdf, bibtex
|
 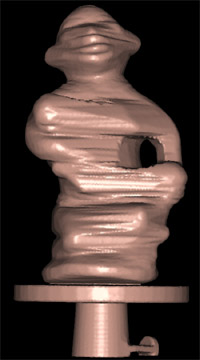 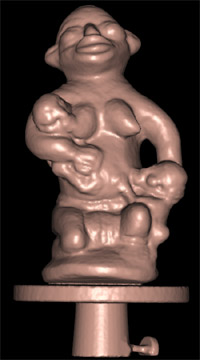  Figure 1. Different steps in the reconstruction process of the Twins model. From left to right: image acquisition, visual hull initialization, shaded final model and textured final model. The reconstructed model has 83241 vertices.
Figure 1. Different steps in the reconstruction process of the Twins model. From left to right: image acquisition, visual hull initialization, shaded final model and textured final model. The reconstructed model has 83241 vertices.
System overview
We present a new approach to high quality 3D object reconstruction. Starting
from a calibrated sequence of color images, the algorithm is able to reconstruct both the 3D geometry and the texture. The core of the method is based on
a deformable model, which defines the framework where texture and silhouette
information can be fused. This is achieved by defining two external forces
based on the images: a texture driven force and a silhouette driven force.
The texture force is computed in two steps: a multi-stereo correlation
voting approach and a gradient vector flow diffusion. Due to the high resolution of the voting approach, a multi-grid version of the gradient vector flow has been developed. Concerning the silhouette force, a new formulation of the silhouette constraint is derived. It provides a robust way to integrate the silhouettes in the evolution algorithm. As a consequence, we are able to recover the apparent contours of the model at the end of the iteration process. Finally, a texture map is computed from the original images for the reconstructed 3D model.
The deformable model framework allows us to define an energy functional that takes into account all the information that we want to use. The final surface is then defined as the minimal surface that minimizes this functional. If we use an explicit solution of the minimization problem, we get at the kth iteration:
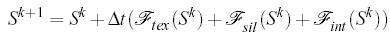 ,
where ,
where 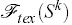 is the stereo force,
is the stereo force, 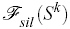 is the silhouette force and
is the silhouette force and 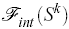 is the internal force.
is the internal force.
To completely define the deformation framework, we need an initial value
of S, i.e., an initial surface S0 that will evolve under the
different energies until convergence.
If we make a list of possible initializations, we can establish an ordered
list, where the first and simplest initialization is the bounding box of
the object. The next simplest surface is the convex hull of the object.
Both the bounding box and the convex hull are unable to represent surfaces
with a genus greater than 0. A more refined initialization, which lies
between the convex hull and the real object surface is the visual hull.
Visual Hull construction
The method used to construct the visual hull is based on a space carving
method. The silhouettes of the object allow to define an implicit function,
the visual hull being the isolevel 0 of this function. The result of this
method is an octree surface that can be polygonized by a marching cube
or marching tetrahedron algorithm.
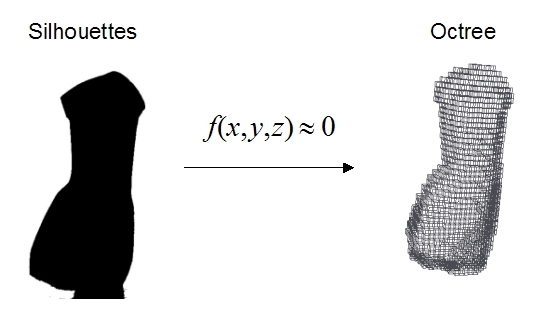
Figure 2. Visual Hull computation by the definition of an isolevel function.
We can see an example of how the marching tetrahedron triangulation
works:
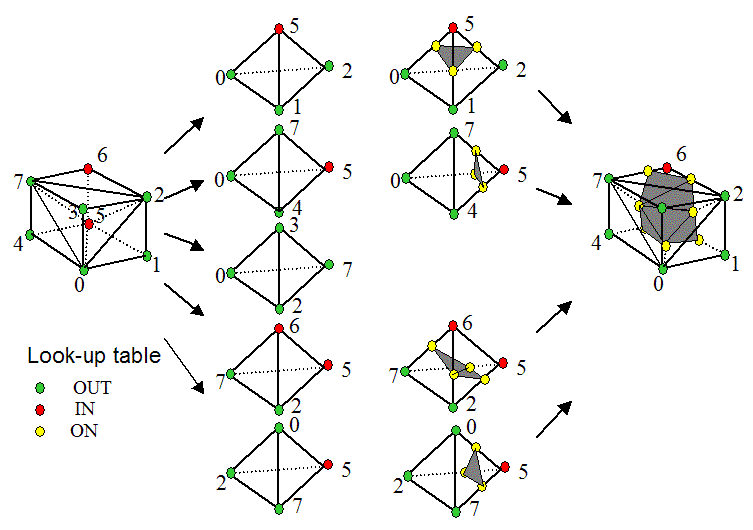 Figure 3. Marching cube using a tetrahedron decomposition.
Figure 3. Marching cube using a tetrahedron decomposition.
Stereo force
Multi-stereo correlation
A simple and robust way to exploit the stereo information of multiple images
consists of estimating for every pixel of every image the depth to the real
surface by a multi-stereo correlation algorithm. Instead of storing the
depths in a depth buffer per image, all the estimations are stored in a
unique 3D volume, which for efficiency reasons is in fact an octree volume.
Using a 3D volume allows us to take advantage of the voting approach intrin
sic to the use of a 3D grid, which makes the correlation approach more
robust in the presence of highlights. The knowledge of the visual hull,
which is an upper bound of the real object, greatly reduces the stereo
computation time since it reduces the search length of the correlation
algorithm.
The result of the multi-stereo voting approach is a 3D volume that contains
the integral of all the stereo correlations, weighted by the correlation
score.
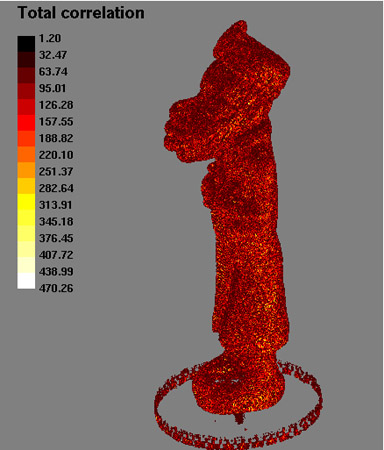  Figure 4. Left: stereo correlation volume of the bigHead model. Right: same view rendered by estimating the surface normal.
Figure 4. Left: stereo correlation volume of the bigHead model. Right: same view rendered by estimating the surface normal.
Multi-resolution Gradient Vector Flow computation
The stereo correlation voting volume can not be used by itself as a deformable
model force because it is a scalar field. Instead we could use its gradient.
But this is a too local force. An even better option being the so called
Gradient Vector Flow. This is a gradient field that is smoothed by a Laplacian
operator. The smoothing operation allows at the same time the propagation
of the gradient information beyond its local definition, improving its
capture range. Since the 3D volume is in fact a multi-resolution volume
(octree), the computation of the GVF is not so easy, and special attention
has to be paid to the resolution changes inside the octree volume.
 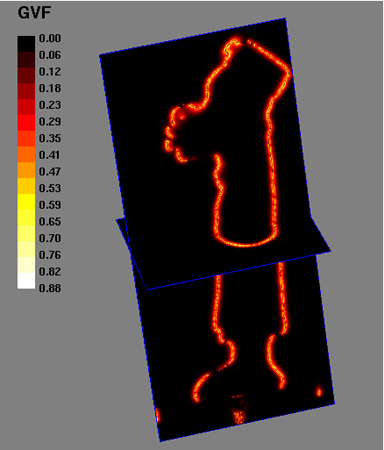
 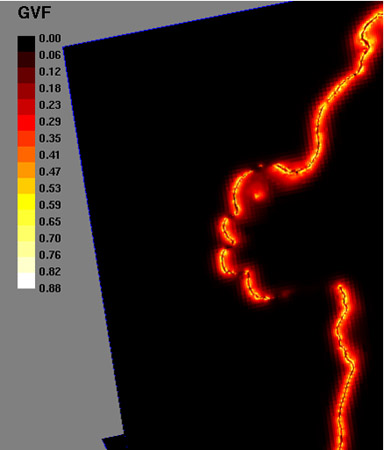 Figure 5. Stereo force used in the reconstruction of the bigHead
model. Top left: the octree partition used in the computation of the gradient
vector flow field. Top right: norm of the gradient vector flow field. Bottom:
details.
Figure 5. Stereo force used in the reconstruction of the bigHead
model. Top left: the octree partition used in the computation of the gradient
vector flow field. Top right: norm of the gradient vector flow field. Bottom:
details.
Silhouette force
The silhouette force is defined as a force that makes the snake match the
original silhouettes of the sequence. If it is the only force of the snake,
the model should converge towards the visual hull. Since we are only interested
in respecting silhouettes, the force will depend on the self occlusion
of the snake. If there is a part of the snake that already matches a particular
silhouette, the rest of the snake is not concerned by that silhouette,
since the silhouette is already matched.
The main problem is how to distinguish between points that have to verify
the silhouettes and those that have not. This is equivalent to finding the apparent contours of the object. The silhouette force can be in fact decomposed into two different components: a component that measures the silhouette fitting, and a component that measures how strongly the silhouette force should be applied. The first component is defined as a distance to the visual hull. The second component measures the occlusion degree of a point of the snake for a given view point. This view point is chosen as the camera that defines the distance to the visual hull. The final silhouette force for a given point of the snake is a vector directed along the normal to the snake surface and its magnitude is the product of both components.
Internal force
In addition to the stereo and silhouette forces, a simple barycentric force
is used as internal force.
Results
  Figure 6. BigHead model after convergence (114496 vertices).
Figure 6. BigHead model after convergence (114496 vertices).
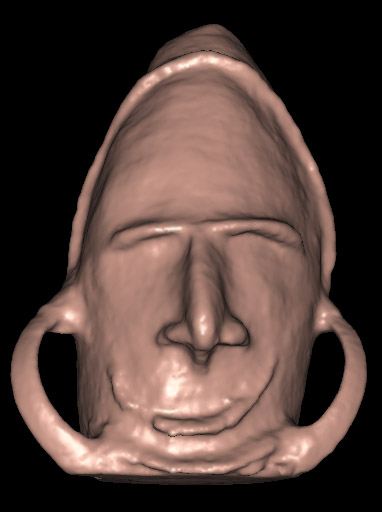  Figure 7. Oceania model after convergence (45843 vertices).
Figure 7. Oceania model after convergence (45843 vertices).
  Figure 8. Thomas Henry model after convergence (83628 vertices).
Figure 8. Thomas Henry model after convergence (83628 vertices).
A 3D repository containing some models reconstructed with this technique
is available at the following address:
http://www.tsi.enst.fr/3dmodels
Acknowledgements: This work has been partially supported by the
SCULPTEUR European project IST-2001-35372. We thank the Thomas Henry museum
at Cherbourg for the image sequences corresponding to Oceania and Thomas
Henry.
|